Notas sobre Processamento Térmico de Alimentos
João Freire de Noronha
Escola Superior Agrária de Coimbra, 1999
A utilização de altas temperaturas é um dos métodos mais utilizados para a preservação de alimentos. Alimentos de grande consumo tais como o leite e enlatados são submetidos a um tratamento térmico destinado à redução da carga microbiana o que permite um aumento do tempo de vida do alimento.
Dependendo dos objectivos do tratamento térmico e da sua intensidade podemos dividir os tratamentos térmicos em três categorias: O escaldão cujo principal objectivo é inactivar enzimas que podem levar à deterioração do alimento durante armazenamento, sendo utilizado também como tratamento preliminar a outros métodos de preservação; a pasteurização, um tratamento térmico destinado à destruição dos microorganismos patogénicos existentes no alimento e a esterilização, um processamento térmico severo que leva à destruição de todos os microorganismos (patogénicos e outros) presentes no alimento capazes de se desenvolverem nas condições esperadas de armazenamento, ou seja que leva à denominada "esterilização comercial".
De modo a compreender os processos de conservação baseados na utilização de altas temperaturas (processamento térmico, ou tratamentos térmicos) é necessário por um lado conhecer qual o efeito das altas temperaturas sobre os microorganismos, enzimas e o que designaremos genericamente por factores de qualidade e por outro lado compreender os mecanismos básicos de transferência de calor do meio de aquecimento (água ou vapor de água) para o alimento e no interior do alimento. Só um conhecimento destes factores nos permitirá o estabelecimento de tratamentos térmicos que levem à produção de alimentos seguros que tenham aceitabilidade por parte do consumidor.
Efeito das altas temperaturas sobre os microorganismos, enzimas e factores de qualidade.
Temperaturas Constantes
É facto conhecido que a exposição de suspensões de microorganismos a temperaturas elevadas leva a uma diminuição do seu número. É também facto conhecido que, para uma dada temperatura, quanto maior o período de aquecimento mais extensa a diminuição observada. A colecção de um elevado número de resultados em experiências em que foram quantificados o número de microorganismos presentes numa dada suspensão quando esta é sujeita a diferentes tempos de aquecimento (a temperatura constante) permitiu concluir que a utilização de uma equação cinética de 1º ordem descreve de um modo aproximado a evolução do número de microorganismos numa dada suspensão ao longo do tempo:
![]() (1)
(1)
onde N, representa o número ou concentração de microorganismos, t o tempo e kT é uma constante (constante cinética da reacção, característica de um dado microorganismo para uma determinado meio e dependente da temperatura) com unidades tempo-1.
A integração da Eq. 1 permite-nos chegar a uma expressão que nos permite calcular o número de microorganismos presentes numa dada suspensão de microorganismos (Nf) quando esta é aquecida a uma temperatura constante por um dado período de tempo (t), dado o número inicial de microorganismos (N0):
![]() (2)
(2)
equivalente a,
![]() (3)
(3)
(sugestão: tente chegar a estas equações)
Uma análise cuidada da Eq. 7 permite-nos no entanto (mesmo antes de efectuar a integração) chegar a uma conclusão importante. Segundo este modelo a taxa de destruição dos microorganismos é em cada instante proporcional ao número de microorganismos presentes. Logo como ao longo do aquecimento o número de microorganismos (N) vai diminuir a taxa de destruição (número de microorganismos destruídos por unidade de tempo) vai necessariamente diminuir. Isto implica que quando o número de microorganismos se aproxima de zero a taxa de destruição também se aproxima de zero, isto é, nunca (de acordo com este modelo) conseguimos atingir a destruição completa dos microorganismos!
Em vez da utilização do valor k é mais usual a utilização do valor D, valor que tem unidades de tempo e que representa o tempo necessário para a redução do número de microorganismos para um décimo do seu valor, para uma dada temperatura, T. A relação entre o valor k e D é dada pela seguinte equação.
![]() (4)
(4)
(sugestão: tente chegar a esta equação)
Tal como o valor k, o valor D é característico para uma dada população de microorganismos num meio determinado e é dependente da temperatura. Na tabela 1 são apresentados alguns valores D para células vegetativas e esporos de microorganismos. Notar a maior resistência dos esporos ao calor.
É assim possível derivar uma equação que nos permita calcular o tempo necessário (a temperatura constante) para reduzir o número (ou concentração) de microorganismos de um dado valor inicial N0 para um valor final, Nf, conhecido o tempo de redução decimal, D:
![]() (5)
(5)
(sugestão: tente chegar a esta equação)
Tabela 1 - Exemplos de valores D para células vegetativas e esporos de bactérias, leveduras e fungos (adaptado de, Gaze, Joy. Principles of calculating Pasteurisation P-Values in Thermal Processing Principles, Practicalities and Calculation- Course Notes. Campden and Chorleywood Food Research Association, UK, 1995)
|
|
Meio |
Temperatura (ºC) |
D (min) |
|
Células Vegetativas |
|
|
|
|
Enterococcus faecalis |
Peixe |
60 |
15.7 |
|
Staphylococcus aureus |
Sopa de ervilhas |
60 |
10.4 |
|
Salmonella senftenberg |
Sopa de ervilhas |
60 |
10.6 |
|
Lactobacillus plantarum |
Sumo de tomate |
70 |
11.0 |
|
Listeria monocytogenes |
Cenoura |
70 |
0.3 |
|
Esporos de Bactérias, leveduras e fungos |
|
|
|
|
Clostridium botulinum |
|
|
|
|
não proteolítico E |
água |
80 |
3.3 |
|
Clostridium butyricum |
Tampão pH 7.0 |
85 |
23 |
|
Byssochlammys fulva |
Sumo de uva |
93 |
5.0 |
|
Zygosaccharomyces bailii |
Caldo |
60 |
8.1 |
O simples modelo que apresentámos permite prever a evolução não só do número de microorganismos (bactérias e seus esporos) mas também, com a utilização de valores D adequados, prever a destruição (inactivação) de enzimas e de outros componentes dos alimentos (vitaminas, factores anti-nutricionais, etc..), tendo sido utilizado com algum sucesso para modelizar as modificações em características organolépticas dos alimentos (cor, textura, etc.). Cabe no entanto aqui frisar que se trata somente de um modelo empírico (i.e. sem uma base teórica subjacente) que nos tem permitido fazer previsões com um grau de precisão adequado num elevado número de situações mas que não é de modo nenhum um modelo adequado a todas as situações, devendo a sua validade ser testado quando utilizado em novas situações.
O efeito da temperatura
A introdução do índice T nos símbolos kT e DT , impõe-se para tornar claro que os valores D e k são dependentes da temperatura. Em tratamentos térmicos em que não possamos considerar que a temperatura se mantêm constante ao longo do tempo (por exemplo a temperatura no centro de uma cenoura mergulhada em água a ferver irá variar ao longo do tempo) não é possível passar da Eq. 1 à Eq. 2 uma vez que o valor de k não é uma constante mas sim uma função da temperatura, i.e. k(T). O mesmo se poderá dizer da aplicabilidade da Eq. 5 uma vez que D varia com a temperatura.
Quando consideramos casos em que há uma variação da temperatura ao longo do processo (e aqui convêm sublinhar que não estamos interessados na temperatura do meio de aquecimento mas sim na temperatura observado no alimento visto ser esta última a temperatura a que os microorganismos estarão sujeitos) teremos de considerar uma das seguintes equações para o cálculo da evolução do número de microorganismos (ou outro factor) ao longo do processo:
![]() (6)
(6)
![]() (7)
(7)
Uma análise cuidada destas equações mostra-nos que temos pela frente dois problemas a resolver de modo a podermos integrar estas equações: O primeiro será o de encontrar expressões que nos permitam calcular os valores de k e de D para diferentes temperaturas, problema que será discutido em seguida. O segundo problema é determinar a evolução da temperatura ao longo do tempo. No exemplo que referimos a temperatura no centro da cenoura é uma função do tempo, T(t), logo os valores de k e de D serão melhor expresso como k(T(t)) e D(T(t)) respectivamente. Esqueçamos por enquanto o problema da determinação de T(t) e concentremo-nos nas soluções encontradas para k(T) e D(T).
Existem dois modelos empíricos que permitem explicar a influência da temperatura na constante cinética da reacção: O modelo de Arrhenius e o modelo proposto por Bigelow (também conhecido por modelo TDT, do inglês, thermal death time).
Segundo o modelo de Arrhenius a dependência de k com a temperatura é dada pela seguinte equação:
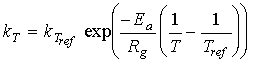 (8)
(8)
sendo Ea (J/mol) a energia de activação, Rg (8.314 J/mol/K) a constante universal dos gases perfeitos e kTref (s-1) a constante cinética da reacção a uma dada temperatura de referência, Tref.
Segundo o modelo de Bigelow o efeito da temperatura na taxa de destruição de microorganismos é expresso pela seguinte equação,
![]() (9)
(9)
sendo z (C°) o número de graus Celsius necessários para modificar o valor de D por um factor de dez e DTref (min) o valor D à temperatura Tref.
(sugestão: verificar que o valor z representa uma diferença de temperatura que leva a uma aumento ou diminuição de DT por um factor de 10)
Como já foi referido ambos os modelos são intrinsecamente empíricos quando utilizados para modelizar a dependência com a temperatura da constante cinética da reacção de morte térmica de destruição de microorganismos. Apesar de preferências individuais por um dos modelos não existem bons argumentos científicos que nos permitam decidir a favor de um deles. Quando são consideradas gamas limitadas de temperaturas, as reduzidas diferenças nos resultados dos dois modelos em conjunção com os erros experimentais dos dados utilizados para os testar não permitem uma escolha categórica a favor de um deles. Ambos têm tido utilizados com sucesso na modelização da degradação térmica de microorganismos, enzimas e factores de qualidade. Por razões históricas o modelo proposto por Bigelow tem sido mais utilizado na indústria alimentar pelo que o utilizaremos preferencialmente no restante deste apontamentos.
Na tabela 2 são apresentam-se valores os valores de z e D121ºC para alguns microorganismos e factores de qualidade, notar que em geral os valores z para os factores de qualidade apresentam valores z superiores aos observados na destruição de microorganismos e seus esporos. Isto significa que a taxa de destruição de microorganismos é mais sensível a aumentos de temperatura que taxa de destruição dos factores de qualidade. Este facto torna possível a optimização dos tratamentos térmicos tema que discutiremos noutro local.
Tabela 2 - Parâmetros de resistência térmica (D e z) para microorganismos e factores de qualidade.
|
|
|
|
|
|
Gama de temperaturas |
|
Clostridum botulinum |
|
|
|
|
|
|
Bacillus stearothermophilus |
|
>4.5 |
4.0-5.0 |
7.0-12.0 |
110-130 |
|
Ácido Ascórbico |
Ervilhas enlatadas |
|
921 |
17.8 |
110-138 |
|
Tiamina |
Carne de vaca |
|
254 |
25.4 |
121-138 |
|
Tiamina |
Puré de ervilhas |
|
247 |
25.2 |
121-138 |
|
Folatos |
Sumo de maçã |
3.4 |
492 |
35.2 |
100-140 |
|
Clorofila |
Ervilhas, escaldadas |
|
13.4 |
43.5 |
115-138 |
|
Clorofila a |
Espinafres |
natural |
13.0 |
25.6 |
116-126 |
|
Escurecimento não enzimático |
|
|
|
|
|
|
Vitamina B6 |
Couve Flor |
|
411 |
50.7 |
105-138 |
|
Vitamina A |
Fígado de vaca |
|
43.5 |
26.0 |
102-127 |
|
Anticianinas |
Uva "Concord" |
3.4 |
123 |
53.4 |
76-121 |
O Valor F
Estamos agora na posse dos conhecimentos necessários que nos permitem derivar uma expressão para o cálculo da redução na população microbiana (ou por outras palavras o impacto do processo) em processos em que a temperatura varia ao longo do tempo.
Substituindo na Eq. 7, DT pelo dependência proposta por Bigelow (Eq. 9) e procedendo à integração da expressão resultante obtemos o seguinte resultado:
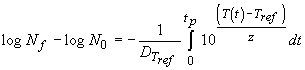 (10)
(10)
sendo N0 o número inicial de microorganismos, Nf o número de microorganismos presentes no final do processo e tp (min) o tempo total de processamento.
(sugestão: tente chegar a esta equação)
Esta expressão fornece-nos um meio de calcularmos o efeito do um dado perfil de tempo-temperatura, T(t), numa dada população de microorganismos. Para um tratamento térmico a temperatura constante esta última equação reduz-se à Eq. 5.
(sugestão: verifique esta última afirmação tendo em atenção a Eq. 9)
Rearranjando esta última equação podemos derivar a seguinte expressão que nos permite calcular o impacto de qualquer tratamento térmico, sobre uma dada população microbiana cuja morte térmica seja caracterizada pelos valores DTref e z:
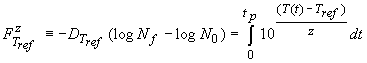 (11)
(11)
sendo ![]() (min) o valor do processo.
(min) o valor do processo.
Por analogia com a Eq. 5 podemos concluir que o valor F representa o tempo de um tratamento térmica a temperatura constante Tref que tem o mesmo impacto sobre a população de microorganismos que uma dado tratamento térmico caracterizado pelo perfil de temperatura, T(t). O valor F tem uma importância para a avaliação de processos existentes e estabelecimento de novos processos térmicos, uma vez que nos permite comparar o efeito de diferentes perfis de tempo-temperatura em termos de impacto sobre a população microbiana. Quanto maior o valor F maior a redução na população de microorganismos. O valor F é denominado por valor do processo, ou valor de esterilização.
A Eq. 11 permite-nos calcular o impacto de uma dado tratamento térmico de dois modos distintos. O primeiro baseado na medição das carga iniciais e finais (antes e apôs tratamento) de microorganismos no produto (N0 e Nf) e o segundo baseado no conhecimento completo do perfil de tempo-temperatura a que o alimento é sujeito, T(t), durante o tratamento.
Considerando o modelo de Arrhenius podemos seguindo um raciocínio análogo derivar a seguinte expressão alternativa para o cálculo do valor F:,
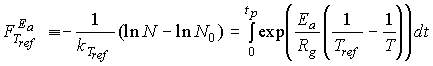 (12)
(12)
O Valor F0
Os tratamentos térmicos de esterilização são normalmente concebidos de modo a reduzir para níveis seguros o número de esporos de Clostridium botulinum, que de outro modo poderiam germinar e levar ao desenvolvimento desta bactéria que é responsável pela produção de uma potente neurotoxina responsável pelo Botulismo, uma doença que pode levar à morte.
A destruição dos esporos de C. botulinum pelo calor obedece a uma cinética de primeira ordem caracterizada por um valor D121.1ºC=0.2 min e por uma valor z=10Cº. Dada a importância deste microorganismo a avaliação do impacto dos processos de esterilização é efectuada usualmente considerando uma temperatura de referência de 121.1ºC e um valor z=10Cº, sendo utilizado neste caso especifico o símbolo F0, i.e.,
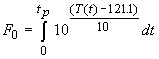 (13)
(13)
Para a avaliação do impacto de um dado tratamento térmico em atributos organolépticos ou em factores de qualidade é utilizada normalmente uma temperatura de referência de 100ºC e valores z na gama 20-40Cº. Neste caso o símbolo F é substituído pelo símbolo C (inicial de cook value).
Estimação "pontual" do impacto do processo vs. estimação volumétrica
A Eq. 13 permite-nos calcular o impacto do processo a partir do conhecimento da história de temperaturas T(t). No caso do aquecimento de um liquido perfeitamente agitado podemos considerar que num dado momento a temperatura é a mesma em todos os pontos e assim calcular o impacto do processo utilizando directamente esta equação. Na maior parte das situações práticas este não é o caso, os diferentes pontos do alimento estão ao longo do tratamento sujeitos a diferentes perfis de tempo-temperatura, o que leva a que o impacto do processo seja diferente nos diferentes pontos do alimento.
De modo a calcular o impacto do processo na totalidade do alimento será então necessário considerar o impacto do processo em cada unidade elementar de volume (em cada ponto, utilizando a Eq. 11 ou 12) e integrar (somar) o efeito ao longo do volume total do alimento de modo a calcular o impacto do processo na totalidade do alimento. Considerando o modelo D-z (modelo de Bigelow) podemos derivar a seguinte expressão para o cálculo do valor do processo integrado para todo o alimento:
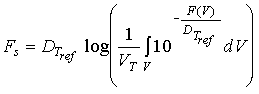 (14)
(14)
onde, F(V) (min) é o valor de esterilização no volume elementar dV e Fs (min) o valor de esterilização para o volume total (ou massa total) do alimento
Esta última equação deveria ser sempre utilizada para o cálculo do impacto de um dado tratamento no número de microorganismos ou em factores de qualidade sempre que não seja realista considerar uma distribuição homogénea de temperatura no alimento ao longo do processo. No entanto, e salvo raras excepções, não nos é possível conhecer a evolução da temperatura com o tempo em todos os pontos do alimento, ou sendo possível a sua determinação, ela é demasiado trabalhosa.
Tendo em vista a falta de informação relativa à evolução da temperatura em todos os pontos do alimento opta-se geralmente por calcular o impacto do processo utilizando a informação relativa a um único ponto no alimento. Quando estamos interessados em calcular o impacto de um dado tratamento térmico sobre uma população de microorganismos calculamos o valor do processo, utilizando por exemplo a Eq. 13, no ponto no alimento que demora mais tempo a aquecer, o denominado "ponto frio" (cold spot), ponto crítico ou ponto de menor letalidade. Este modo de actuação pode ser justificado do seguinte modo: se o alimento sofre um processamento suficientemente severo para reduzir a população microbiana a níveis aceitáveis no ponto que recebe menor quantidade de calor então todos os outros pontos do produto receberão necessariamente um tratamento adequado. Outro argumento a favor deste modo de cálculo prende-se com o facto de na prática não conhecermos a distribuição espacial dos microorganismos no interior do alimento, logo assumindo que todos os microorganismos se encontram no ponto crítico e considerando um tratamento suficientemente severo neste ponto para reduzir o número de microorganismos para um valor aceitável estaremos necessariamente a produzir um alimento seguro.
De modo a estimar o impacto do processo em termos da destruição de factores de qualidade o cálculo do valor C (cook value) pode ser aproximado pelo valor C à superfície do alimento (notar que nos processos clássicos de aquecimento a maior degradação da qualidade do produto será observada à superfície dado ser aqui que o alimento estará sujeito a temperaturas mais altas por maiores períodos de tempo).
O Método Geral
Referimos acima que para integrarmos as Eqs. 6 e 7 seria necessário encontrar expressões que nos permitissem calcular os valores de k e de D para diferentes temperaturas, problema que já resolvemos. Outro problema aí levantado relacionava-se com a necessidade da determinação da evolução da temperatura no alimento ao longo do tempo.
O modo mais simples de resolver este segundo problema passa pela determinação experimental do perfil de tempo-temperatura no interior dos alimentos e posterior integração de, por exemplo, a Eq. 13. Este método para o cálculo do valor do processo, F0, é comummente denominado por Método Geral.
Existem várias maneiras de levar a cabo a integração referida no parágrafo anterior. Apresentamos de seguida algumas maneiras de levar a cabo a integração.
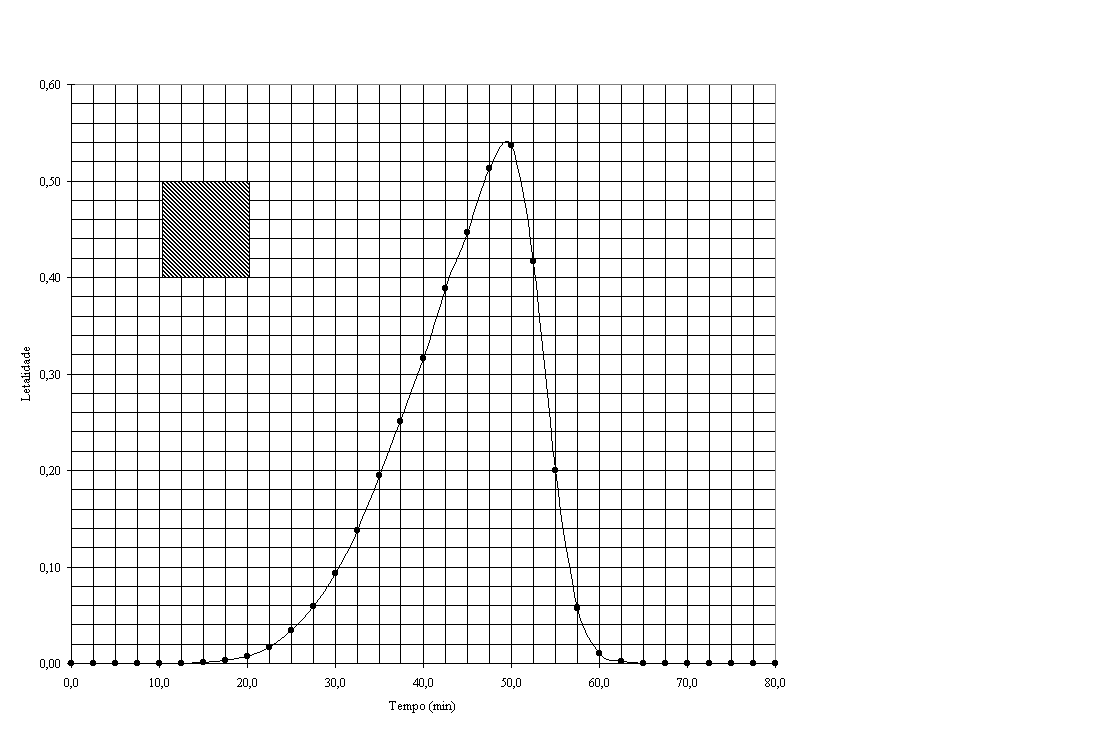
Integração Gráfica
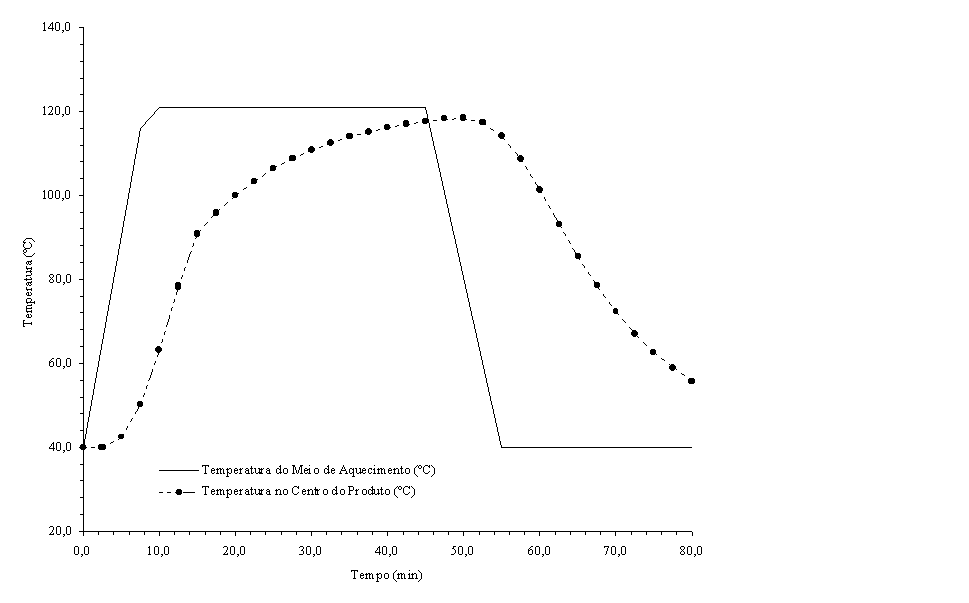
Consideremos o seguinte perfil de temperaturas